트리의 지름
BOJ 1967: 트리의 지름에 대한 설명
저희가 구하고자 하는 트리의 지름은 트리에 “존재하는 모든 경로들 중에서 가장 긴 것의 길이”입니다.
이 길이를 구하기 위해 알고리즘 및 세부 설명을 하겠습니다.
알고리즘 구조
먼저 수도 코드는 다음과 같습니다
- 첫번째 node $x$를 선택한다.
- node $x$로 부터 가장 먼 node $y$를 구한다.
- node $y$로 부터 가장 먼 node $z$를 구한다.
알고리즘 설명
이 알고리즘이 왜 답을 찾는 방식인지 설명하도록 하겠습니다.
트리가 존재한다고 할 때, 트리의 지름에 대한 node를 $u, v$라고 설정합니다.
그리고, 선택한 node $x$와 가장 길이가 긴 node $y$를 구합니다.
이때, node $x,y,u,v$에 대해 3가지 경우의 수로 나눌 수 있습니다.
- $x$가 $u, v$ 두가지 node중 하나이다.
- $y$가 $u,v$ 두가지 node중 하나이다.
- $x,y$가 $u,v$ 와 전혀 다를 경우
1번과 2번 케이스의 경우, $x,y$로 부터 $u,v$를 찾을 수 있습니다.
왜냐하면,
1번 케이스일 때, $x$로 부터 가장 먼 node $y$이며, $x$가 $u,v$에 포함되기 때문에, $x,y$가 $u,v$와 동일합니다.
2번 케이스라면, $y$로 부터 가장 먼 node는 $z$이며, $y$가 $u,v$에 포함되기 때문에, $y,z$가 $u,v$와 동일합니다.
1,2번 케이스를 제외한 3번 케이스에 대해 설명하도록 하겠습니다.
3번 케이스는 다시 2가지 세부 케이스로 나눠지게 되는데
3-1. $x,y$와 $u,v$가 1개 이상의 접점 node을 가진다.
3-2. $x,y$와 $u,v$가 전혀 접점 node를 가지지 않는다.
3-1의 경우, 이미지로 표현한다면, 다음과 같이 표현할 수 있습니다.
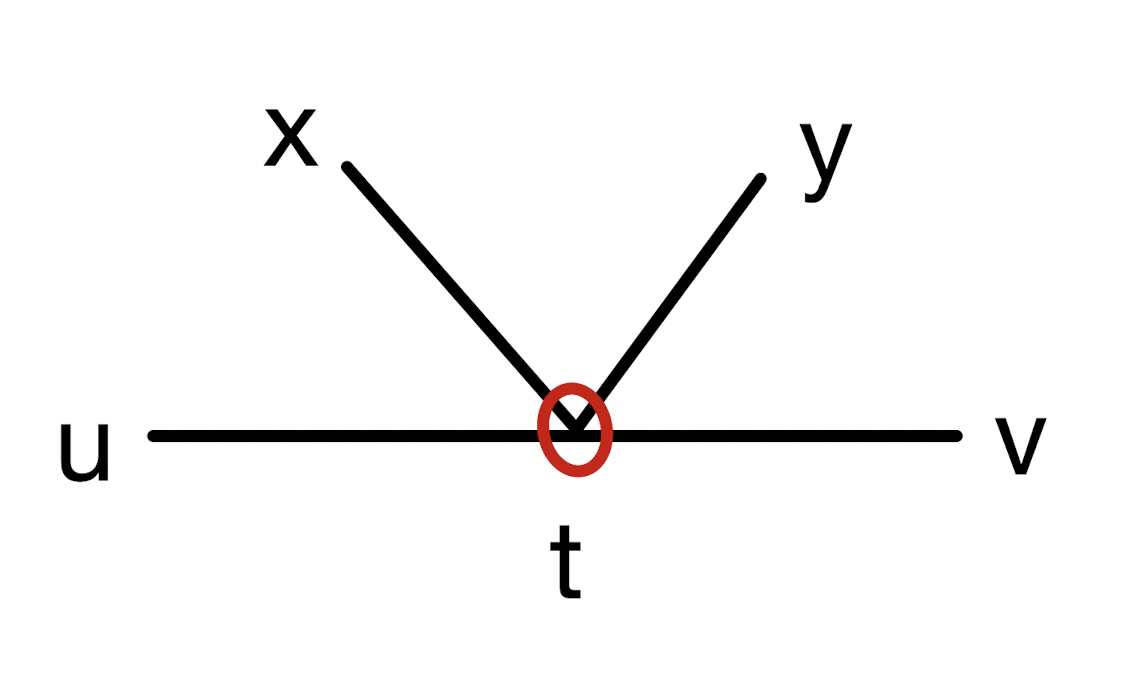
$d(x,t)$를 $x$와 $t$사이의 길이라고 표시하겠습니다.
그러면, $x$에서 가장 먼 node는 $y$이고, 두 점의 길이는 $d(x,y) = d(x,t)+d(t,y)$입니다.
이때, $x$에서 가장 긴 길이는 $u$와 $v$가 아닌 $y$이기 때문에, $d(t,y)\geq d(u, t)$ 또는 $d(t,y)\geq d(t,v)$가 되어야 합니다.
그러면, 트리에서 가장 긴 경로라고 가정한 $u$와 $v$의 길이 $d(u,v) = d(u,t) + d(t,v)$ 보다 더 큰 길이 $d(y,v) = d(t,y) + d(t,v)$ 또는 $d(u,y) = d(u,t) + d(t,y)$가 존재하게 됩니다.
따라서, 지름은 $d(u,v)$가 아닌 $d(y,v)$ 또는 $d(u,y)$가 되고, 2번 케이스 “$y$가 $u,v$ 두가지 node중 하나이다.”에 포함됩니다.
3-2의 경우, 문제에서 제시한 “트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다”에 반한 조건이므로 존재할 수 없습니다.
따라서, $x,y,z$를 통해 가장 긴 길이를 구하는 것이 트리의 지름을 구하는 것이라고 할 수 있습니다.
아래에는 해답 code입니다.
find_far 현재 node로 부터 가장 길이가 먼 node를 bfs로 찾는 함수입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
N = int(input())
tree_node = [[] for _ in range(N+1)]
for i in range(N-1):
a,b,c = map(int, input().split())
tree_node[a].append([b,c])
tree_node[b].append([a,c])
def find_far(init_node):
is_check = [False]*(N+1)
is_check[init_node] = True
Q = [[init_node,0]]
max_dis = [init_node, 0]
while Q:
node, dis = Q.pop(0)
for next_node, cost in tree_node[node]:
if not is_check[next_node]:
is_check[next_node] = True
Q.append([next_node, dis+cost])
if max_dis[1] < dis + cost:
max_dis = [next_node, dis + cost]
return max_dis
y = find_far(1)[0]
print(find_far(y)[1])
참고: blog.myungwoo.kr.